파이썬으로 순열, 조합, 중복순열, 중복조합 경우의 수 구하기!
순열
n개 중 서로 다른 r개를 뽑아서 줄 세우는 경우의 수
nPr = n! / (n-r)!
조합
n개중 서로 다른 r개를 뽑기만 함
nCr = n! / (n-r)!*r!
순열, 조합을 구하는 방법
#from itertools import permutations, combinations, product, combinations_with_replacement
import itertools
data = ['A', 'B', 'C']
#순열
print(list(itertools.permutations(data,3)))
#조합
print(list(itertools.combinations(data,2)))
#중복순열
print(list(itertools.product(data,repeat = 2)))
#중복조합
print(list(itertools.combinations_with_replacement(data,2)))결과 >>
[('A', 'B', 'C'), ('A', 'C', 'B'), ('B', 'A', 'C'), ('B', 'C', 'A'), ('C', 'A', 'B'), ('C', 'B', 'A')]
[('A', 'B'), ('A', 'C'), ('B', 'C')]
[('A', 'A'), ('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'B'), ('B', 'C'), ('C', 'A'), ('C', 'B'), ('C', 'C')]
[('A', 'A'), ('A', 'B'), ('A', 'C'), ('B', 'B'), ('B', 'C'), ('C', 'C')]
만약 조합의 경우의 수를 계산하고 싶다면
1) 마찬가지로 itertools를 이용
len(list(combinations(range(n), r)))
2) math 라이브러리를 이용해 팩토리얼로 계산
math.factorial(n) // ( math.factorial(n-r) * math.factorial(r))
수행시간의 경우 factorial로 계산하는 것보다 itertools의 combinations를 이용하는 방식이 더 오래 걸렸음
코드:
import math, itertools, time
n, r = map(int, input().split())
start = time.time()
result1 = math.factorial(n) //( math.factorial(n-r) * math.factorial(r))
end = time.time()
print("factorial:"+ str(result1))
print(end-start)
start = time.time()
result2 = itertools.combinations(range(n), r)
end = time.time()
print("itertools:" + str(len(list(result2))))
print(end-start)
<예시1>
입력값: 5 1
출력:
factorial:5
1.4066696166992188e-05
itertools:5
2.09808349609375e-05
<예시2>
입력값: 29 13
출력:
factorial:67863915
0.00014209747314453125
itertools:67863915
3.409385681152344e-05
<예시3>
입력: 500 137
출력:

정신 못차리죠?
조합 문제 예시
백준 1010 다리 놓기
https://www.acmicpc.net/problem/1010
1010번: 다리 놓기
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
www.acmicpc.net
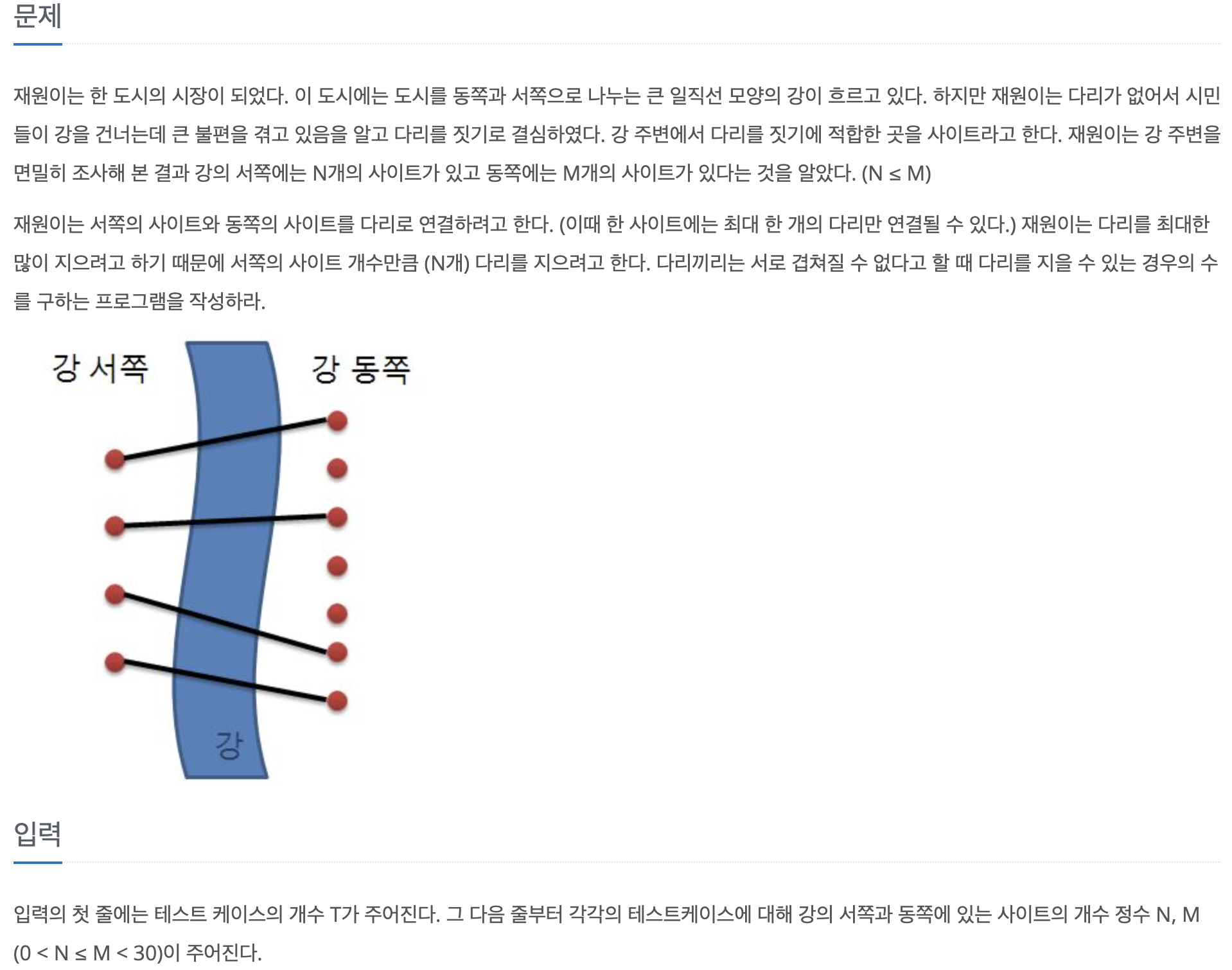
풀이:
다리는 겹쳐서 놓을 수 없고, n <= m이므로
오른쪽의 m개의 다리 중 n개를 선택만 하면 된다
-> 조합으로 풀면 된다!
import math
num = int(input())
for i in range(num):
r, n = map(int, input().split())
print(math.factorial(n) //( math.factorial(n-r) * math.factorial(r)))
'🖥' 카테고리의 다른 글
| [Python] Slice로 부분 리스트, 부분 문자열 구하기 (0) | 2022.05.09 |
|---|---|
| Visual Studio Code에서 탭으로 괄호 밖으로 나가기 (0) | 2022.05.08 |
| 파이썬 주석처리 (한줄, 여러줄, 단축키) (0) | 2022.05.08 |
| [Python] 순열조합 itertools 없이 직접 구현하기 (순열 조합 중복순열 중복조합 ) (0) | 2022.05.03 |
| 파이썬 syntax (0) | 2022.04.29 |


댓글